Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local
%load_ext autoreload
%autoreload 2 
Chapter 6 Overfitting and Advances in Mitigation Techniques
“Simplicity is the ultimate sophistication.” - Leonardo da Vinci
Deep learning models have the powerful ability to express complex functions through numerous parameters. However, this ability can sometimes be a double-edged sword. When a model is overly fitted to the training data, the predictive performance on new data may actually decrease due to the overfitting phenomenon.
Since the resurgence of the backpropagation algorithm in 1986, overfitting has been a relentless challenge for deep learning researchers. Initially, they responded to overfitting by simply reducing the model size or increasing the training data. However, these methods were limited by their restriction on the model’s expressiveness or the difficulty of data collection. The emergence of AlexNet in 2012 opened a new era for deep learning but also highlighted the severity of the overfitting problem. AlexNet had many more parameters than previous models, increasing the risk of overfitting. As the scale of deep learning models increased exponentially thereafter, the overfitting problem became a core challenge in deep learning research.
In this chapter, we will explore the nature of overfitting and various techniques that have evolved to address it. Just as explorers navigate uncharted territories and create maps, deep learning researchers have continuously explored and developed new methods to overcome the obstacle of overfitting.
6.1 Understanding Overfitting
Overfitting was first mentioned in William Hopkins’ writings in 1670, but its modern meaning began with a mention in the Quarterly Review of Biology in 1935: “Analyzing six variables with 13 observations seems like overfitting.” It was formally studied in statistics starting in the 1950s, particularly in the context of time series analysis in the 1952 paper “Tests of Fit in Time Series.”
In deep learning, the overfitting problem entered a new phase with the emergence of AlexNet in 2012. AlexNet was a large-scale neural network with approximately 60 million parameters, unprecedented in scale compared to previous models. As the size of deep learning models increased exponentially thereafter, the overfitting problem became more severe. For example, modern large language models (LLMs) have billions of parameters, making overfitting prevention a core challenge in model design.
In response to these challenges, innovative solutions such as dropout (2014) and batch normalization (2015) were proposed. More recently, methods utilizing training history for overfitting detection and prevention (2024) are being researched. Especially in large models, various strategies are used in combination, from traditional methods like early stopping to modern techniques like ensemble learning and data augmentation.
Let’s intuitively understand the overfitting phenomenon through a simple example. We’ll apply polynomials of different degrees to noisy sine function data.
Code
import numpy as np
import seaborn as sns
# Noisy sin graph
def real_func(x):
y = np.sin(x) + np.random.uniform(-0.2, 0.2, len(x))
return y
# Create x data from 40 to 320 degrees. Use a step value to avoid making it too dense.
x = np.array([np.pi/180 * i for i in range(40, 320, 4)])
y = real_func(x)
import seaborn as sns
sns.scatterplot(x=x, y=y, label='real function')
# Plot with 1st, 3rd, and 21th degree polynomials.
for deg in [1, 3, 21]:
# Get the coefficients for the corresponding degree using polyfit, and create the estimated function using poly1d.
params = np.polyfit(x, y, deg) # Get the parameter values
# print(f" {deg} params = {params}")
p = np.poly1d(params) # Get the line function
sns.lineplot(x=x, y=p(x), color=f"C{deg}", label=f"deg = {deg}")The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload/tmp/ipykernel_1362795/2136320363.py:25: RankWarning: Polyfit may be poorly conditioned
params = np.polyfit(x, y, deg) # Get the parameter values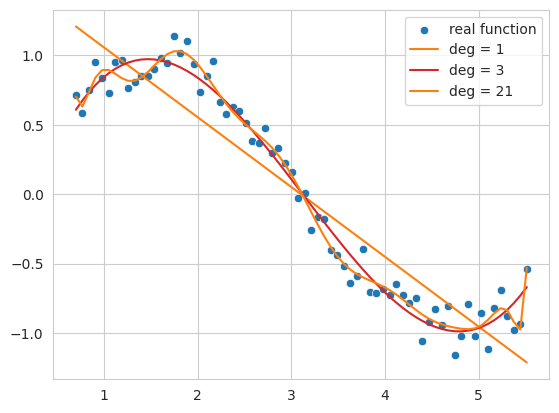
The code above generates noisy sine function data and fits it with 1st, 3rd, and 21st degree polynomials as an example.
1st degree function (deg = 1): The result is a simple line that does not follow the overall trend of the data. This shows a state of underfitting, where the model fails to capture the complexity of the data.
3rd degree function (deg = 3): It follows the basic pattern of the data relatively well, forming a smooth curve without being overly affected by noise.
21st degree function (deg = 21): The result shows overfitting, where the model follows the training data too closely, including its noise, and becomes overly optimized for only the training data.
Thus, if the complexity of the model (the degree of the polynomial in this case) is too low, underfitting occurs; if it’s too high, overfitting occurs. What we ultimately want to find is a model that generalizes well not just to the training data but also to new data - that is, an approximation function closest to the actual sine function.
Overfitting occurs when the complexity (or capacity) of the model is relatively high compared to the amount of training data. Neural networks are especially prone to overfitting because they have many parameters and high expressiveness. Overfitting can also occur when there’s not enough training data or when the data contains a lot of noise. The characteristics of overfitting include:
- Training data loss continues to decrease.
- Validation data loss initially decreases, then starts to increase at some point.
- This is because the model learns not just the underlying pattern but also the noise and fine details of the training data, becoming overly specialized in it.
As a result, an overfitted model performs well on the training data but shows poor prediction performance on new, unseen data. To prevent such overfitting, we’ll explore various techniques like L1/L2 regularization, dropout, and batch normalization in more detail later.
6.2 Regularization Techniques
Challenge: What methods can effectively control the complexity of a model while improving its generalization performance?
Researcher’s Dilemma: Reducing the size of a model to prevent overfitting may limit its expressiveness, and simply increasing the training data is not always possible. It was necessary to impose constraints on the model’s structure or learning process to prevent excessive optimization for the training data and improve predictive performance for new data.
6.2.1 L1, L2 Regularization
In neural networks, L1 and L2 regularization are commonly used. L1 refers to Lasso regression, while L2 refers to Ridge regression.
Ridge regression and Lasso regression introduce a penalty term to restrict parameter movement. The differences between the two methods can be summarized in the following table:
| Feature | Ridge Regression | Lasso Regression |
|---|---|---|
| Penalty Type | Imposes an L2 penalty. The penalty term is the sum of the squares of the parameters multiplied by alpha. | Imposes an L1 penalty. The penalty term is the sum of the absolute values of the parameters multiplied by alpha. |
| Parameter Impact | Suppresses large parameters, making them close to 0, but not exactly 0 | Can set some parameter values to 0 when alpha is large, resulting in a simpler model |
| Overall Impact | Preserves all parameters, including those with minor effects | Selectively retains relevant parameters, allowing for a more straightforward explanation of complex models. |
| Optimization Characteristics | Less sensitive to ideal values compared to Lasso | Sensitive to ideal values due to the absolute value penalty term |
The equations can be expressed as follows:
Ridge Regression Objective Function
“Modified Ridge Objective Function” = (Unmodified Linear Regression Function) + \(\alpha \cdot \sum (\text{parameter})^2\)
\(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2\)
Here, \(\beta\) is the parameter vector being sought. \(\alpha \sum_{j} \beta_{j}^2\) is the penalty term or regularization term. \(\alpha\) is a hyperparameter that controls the size of the regularization term. The formula for obtaining the parameters is as follows.
\(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2 \right)\)
Lasso Regression Objective Function
“Modified Lasso Objective Function” = (Unmodified Linear Regression Function) + $ || $
\(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_{j}|\) \(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_j| \right)\) Using L2 with the sum of the squares of parameters as a penalty term is often referred to as weight decay in neural networks. Let’s take a look at how ridge (L2) regression differs from simple linear regression using sklearn’s implemented model. To do this, we need to increase the dimension of the input x data to the degree. We will use the following simple utility function to create it.
Code
def get_x_powered(x, p=1):
size = len(x)
# The shape of the created x will be (data size, degree)
new_x = np.zeros((size, p))
for s in range(len(x)): # Iterate over data size
for d in range(1, p+1): # Iterate over degrees
new_x[s][d-1] = x[s]**d # Raise x to the power of the degree.
return new_x
# Let's take a quick look at how it works.
deg = 3
x = np.array([np.pi/180 * i for i in range(20, 35, 5)])
y = real_func(x) # real_func는 이전 코드에 정의되어 있다고 가정
print(f"x = {x}")
new_x = get_x_powered(x, p=deg)
print(f"new_x = {new_x}")x = [0.34906585 0.43633231 0.52359878]
new_x = [[0.34906585 0.12184697 0.04253262]
[0.43633231 0.19038589 0.08307151]
[0.52359878 0.27415568 0.14354758]]Because it is third-order, the value of \(x\) increases to \(x^2, x^3\). For example, 0.3490, 0.1218 (the square of 0.3490), and 0.04253 (the cube of 0.3490) are examples. If it is tenth-order, data up to \(x^{10}\) is created. The alpha value of the penalty term can have a value from 0 to infinity. As the alpha value increases, the regulation intensity becomes larger. With the degree fixed at 13, we will compare the linear regression function and ridge regression by changing the alpha value.
Code
import numpy as np
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
# Create a noisy sine wave (increased noise)
def real_func(x):
return np.sin(x) + np.random.normal(0, 0.4, len(x)) # Increased noise
# Create x data (narrower range)
x = np.array([np.pi / 180 * i for i in range(40, 280, 8)]) # Narrower range, larger step
y = real_func(x)
# Degree of the polynomial
deg = 10
# List of alpha values to compare (adjusted)
alpha_list = [0.0, 0.1, 10] # Adjusted alpha values
cols = len(alpha_list)
fig, axes_list = plt.subplots(1, cols, figsize=(20, 5)) # Adjusted figure size
for i, alpha in enumerate(alpha_list):
axes = axes_list[i]
# Plot the original data
sns.scatterplot(ax=axes, x=x, y=y, label='real function', s=50) # Increased marker size
# Plot linear regression
params = np.polyfit(x, y, deg)
p = np.poly1d(params)
sns.lineplot(ax=axes, x=x, y=p(x), label=f"LR deg = {deg}")
# Ridge regression (using Pipeline, solver='auto')
model = make_pipeline(PolynomialFeatures(degree=deg), Ridge(alpha=alpha, solver='auto'))
model.fit(x.reshape(-1, 1), y) # Reshape x for pipeline
y_pred = model.predict(x.reshape(-1, 1)) # Reshape x for prediction
sns.lineplot(ax=axes, x=x, y=y_pred, label=f"Ridge alpha={alpha:0.1e} deg={deg}")
axes.set_title(f"Alpha = {alpha:0.1e}")
axes.set_ylim(-1.5, 1.5) # Limit y-axis range
axes.legend()
plt.tight_layout()
plt.show()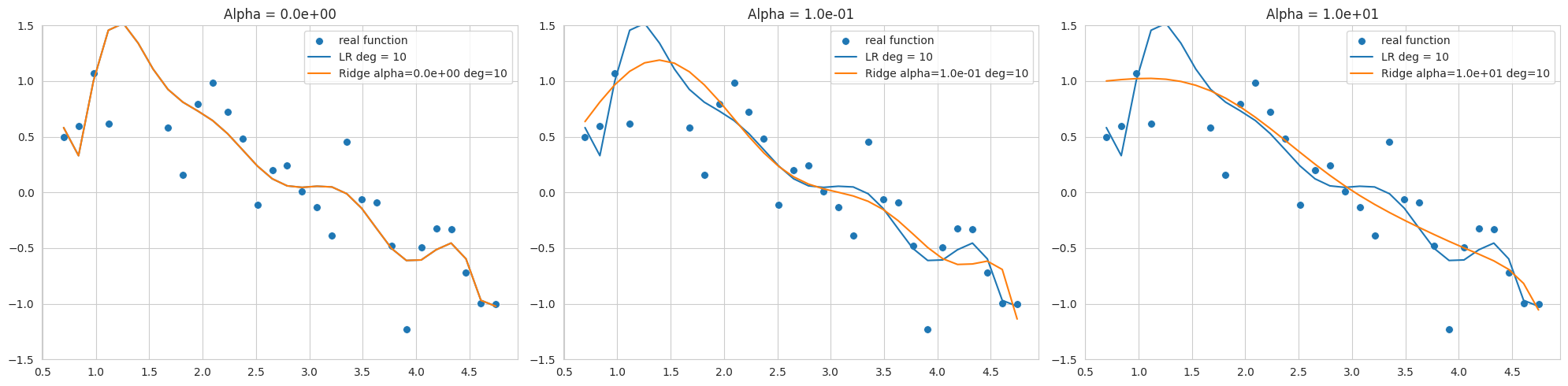
The above graph is the result of fitting a 10th degree polynomial to noisy sine function data, showing Ridge regression results with different alpha values (regularization strengths). The data range is narrow and noisy, so overfitting easily occurs even at low degrees.
- Alpha = 0.0: Ridge regression becomes the same as ordinary least squares linear regression, and the 10th degree polynomial follows the training data noise, showing a severely wavy overfitting shape.
- Alpha = 0.1: Weak regularization is applied, reducing the waviness compared to
alpha=0, but still sensitive to noise and far from the sine function. - Alpha = 10: Strong regularization makes the curve much smoother, well representing the overall trend of the data (sine function). This shows that L2 regularization (Ridge regression) effectively controls overfitting.
By selecting an appropriate alpha value, we can control model complexity and improve generalization performance. L2 regularization is useful for stabilizing models by making weights close to 0.
The sklearn.linear_model.Ridge model can have different optimization methods depending on the solver. Especially when the data range is narrow and noisy like this example, the 'svd' or 'cholesky' solver may be more stable, so careful selection of the solver is necessary (in the code, 'cholesky' is specified).
6.2.2 Applying L1, L2 Regularization in PyTorch
PyTorch and Keras have different ways of implementing L1 and L2 regularization. Keras supports adding regularization terms directly to each layer (kernel_regularizer, bias_regularizer).
Code
# In Keras, you can specify regularization when declaring a layer.
keras.layers.Dense(64, activation='relu',
kernel_regularizer=regularizers.l2(0.01),
input_shape=(784,))On the other hand, PyTorch applies L2 regularization by setting weight decay on the optimizer, and L1 regularization is typically implemented through a custom loss function.
Code
import torch.nn as nn
import torch
def custom_loss(outputs, targets, model, lambda_l1=0.01, lambda_l2=0.01,):
mse_loss = nn.MSELoss()(outputs, targets)
l1_loss = 0.
l2_loss = 0.
for param in model.parameters():
l1_loss += torch.sum(torch.abs(param)) # Take the absolute value of the parameters.
l2_loss += torch.sum(param ** 2) # Square the parameters.
total_loss = mse_loss + lambda_l1 * l1_loss + lambda_l2 * l2_loss # Add L1 and L2 penalty terms to the loss.
return total_loss
# Example usage within a training loop (not runnable as is)
# for inputs, targets in dataloader:
# # ... (rest of the training loop)
# loss = custom_loss(outputs, targets, model)
# loss.backward()
# ... (rest of the training loop)As in the above example, you can define a custom_loss function to apply both L1 and L2 regularization. However, it is common to set the weight_decay corresponding to L2 regularization in the optimizer. But Adam and SGD optimizers implement weight decay slightly differently than L2 regularization. Traditional L2 regularization is to add a parameter squared term to the loss function.
\(L_{n+1} = L_{n} + \frac{ \lambda }{2} \sum w^2\)
Differentiating this with respect to the parameters gives:
\(\frac{\partial L_{n+1}}{\partial w} = \frac{\partial L_{n}}{\partial w} +\lambda w\)
SGD and Adam are implemented by directly adding the \(\lambda w\) term to the gradient. The SGD code in chapter_05/optimizers is as follows.
Code
if self.weight_decay != 0:
grad = grad.add(p, alpha=self.weight_decay)This approach does not have exactly the same effect as adding an L2 regularization term to the loss function when combined with momentum or adaptive learning rate.
AdamW and Decoupled Weight Decay
The 2017 ICLR paper “Fixing Weight Decay Regularization in Adam” (https://arxiv.org/abs/1711.05101) pointed out that weight decay in the Adam optimizer works differently from L2 regularization, and proposed the AdamW optimizer to fix this issue. In AdamW, weight decay is decoupled from gradient updates and applied directly in the parameter update step. The code is in the same basic.py.
Code
# PyTorch AdamW weght decay
if weight_decay != 0:
param.data.mul_(1 - lr * weight_decay)AdamW multiplies the parameter value by 1 - lr * weight_decay.
- Weight decay in existing Adam: The weight decay term (\(\lambda w\)) is considered during the gradient update step along with the learning rate (\(lr\)) and other gradient adjustment terms (e.g., momentum). This causes the effect of weight decay to vary depending on the learning rate and other hyperparameter settings.
- Weight decay in AdamW: Since weight decay is applied separately at the parameter update step, it is less dependent on the learning rate or other hyperparameters. That is, the effect of weight decay becomes more predictable and consistent.
In conclusion, AdamW’s approach is closer to a more accurate implementation of L2 regularization. While it’s common to refer to SGD and Adam’s weight decay as L2 regularization due to historical reasons and similar effects, it’s more accurate to view them as separate regularization techniques, and AdamW clarifies this difference, providing better performance.
6.2.3 Analyzing the Regularization Effect on the Loss Surface
To visually understand the effect of L1 and L2 regularization on model learning, we will use the loss surface visualization technique introduced in Chapter 4. We compare the change in the loss surface with and without L2 regularization and observe how the location of the optimum changes with the strength of the regularization (weight_decay).
Code
import sys
from dldna.chapter_05.visualization.loss_surface import xy_perturb_loss, hessian_eigenvectors, visualize_loss_surface
from dldna.chapter_04.utils.data import get_dataset, get_device
from dldna.chapter_04.utils.metrics import load_model
import torch
import torch.nn as nn
import numpy as np
import torch.utils.data as data_utils
from torch.utils.data import DataLoader
device = get_device() # Get the device (CPU or CUDA)
train_dataset, test_dataset = get_dataset() # Load the datasets.
act_name = "ReLU"
model_file = f"SimpleNetwork-{act_name}.pth"
small_dataset = data_utils.Subset(test_dataset, torch.arange(0, 256)) # Use a subset of the test dataset
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True) # Create a data loader
loss_func = nn.CrossEntropyLoss() # Define the loss function
# Load the trained model.
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU") # 4장의 load_model 사용
trained_model = trained_model.to(device) # Move the model to the device
top_n = 2 # Number of top eigenvalues/eigenvectors to compute
top_eigenvalues, top_eigenvectors = hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True) # 5장의 함수 사용
d_min ,d_max, d_num = -1, 1, 50 # Define the range and number of points for the grid
lambda1, lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32), np.linspace(d_min, d_max, d_num).astype(np.float32) # Create the grid of lambda values
x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eigenvectors, data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device) # 5장의 함수 사용Create an approximate function with xy_perturb_loss, then put (x, y) into the approximate function again to obtain a new z value. The reason for doing this is that when drawing contours with the value obtained by xy_perturb_loss as in Chapter 5, the minimum value is slightly different, so the point of convergence of the optimizer deviates slightly. Now, without expressing all the paths the optimizer takes, only the last lowest point is compared while increasing the weight_decay value.
Code
import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim # Import optim
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, Subset
# 5장, 4장 함수들 import
from dldna.chapter_05.visualization.loss_surface import (
hessian_eigenvectors,
xy_perturb_loss,
visualize_loss_surface
)
from dldna.chapter_04.utils.data import get_dataset, get_device
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.visualization.gaussian_loss_surface import (
get_opt_params,
train_loss_surface,
gaussian_func # gaussian_func 추가.
)
device = get_device()
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()
act_name = "ReLU" # Tanh로 실험하려면 이 부분을 변경
model_file = f"SimpleNetwork-{act_name}.pth"
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU")
trained_model = trained_model.to(device)
top_n = 2
top_eigenvalues, top_eigenvectors = hessian_eigenvectors(
model=trained_model,
loss_func=loss_func,
data_loader=data_loader,
top_n=top_n,
is_cuda=True
)
d_min, d_max, d_num = -1, 1, 30 # 5장의 30을 사용
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)
x, y, z = xy_perturb_loss(
model=trained_model,
top_eigenvectors=top_eigenvectors,
data_loader=data_loader,
loss_func=loss_func,
lambda1=lambda1,
lambda2=lambda2,
device=device # device 추가
)
# --- Optimization and Visualization ---
# Find the parameters that best fit the data.
popt, _, offset = get_opt_params(x, y, z) # offset 사용
print(f"Optimal parameters: {popt}")
# Get a new z using the optimized surface function (Gaussian).
# No need for global g_offset, we can use the returned offset.
z_fitted = gaussian_func((x, y), *popt,offset) # offset을 더해야 함.
data = [(x, y, z_fitted)] # Use z_fitted
axes = visualize_loss_surface(data, act_name=act_name, color="C0", size=6, levels=80, alpha=0.7, plot_3d=False)
ax = axes[0]
# Train with different weight decays and plot trajectories.
for n, weight_decay in enumerate([0.0, 6.0, 10.0, 18.0, 20.0]):
# for n, weight_decay in enumerate([0.0]): # For faster testing
points_sgd_m = train_loss_surface(
lambda params: optim.SGD(params, lr=0.1, momentum=0.7, weight_decay=weight_decay),
[d_min, d_max],
200,
(*popt, offset) # unpack popt and offset
)
ax.plot(
points_sgd_m[-1, 0],
points_sgd_m[-1, 1],
color=f"C{n}",
marker="o",
markersize=10,
zorder=2,
label=f"wd={weight_decay:0.1f}"
)
ax.ticklabel_format(axis='both', style='scientific', scilimits=(0, 0))
plt.legend()
plt.show()Function parameters = [ 4.59165436 0.34582255 -0.03204057 -1.09810435 1.54530407]
Optimal parameters: [ 4.59165436 0.34582255 -0.03204057 -1.09810435 1.54530407]
train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.8065, 0.9251]
SGD: Iter=200 loss=1.9090 w=[0.3458, -0.0320]
train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.2065, 0.3251]
SGD: Iter=200 loss=1.9952 w=[0.1327, -0.0077]
train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.1935, -0.0749]
SGD: Iter=200 loss=2.0293 w=[0.0935, -0.0051]
train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.9935, -0.8749]
SGD: Iter=200 loss=2.0641 w=[0.0587, -0.0030]
train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[1.1935, -1.0749]
SGD: Iter=200 loss=2.0694 w=[0.0537, -0.0027]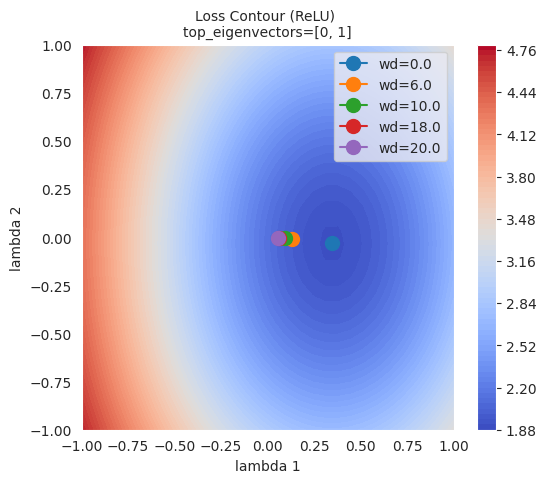
As can be seen in the figure, the larger the L2 regulation (weight decay), the farther the final point reached by the optimizer is from the lowest point of the loss function. This is because L2 regularization helps prevent the model from overfitting by preventing the weights from becoming too large.
L1 regularization creates a sparse model by making some weights 0. It is useful when you want to reduce the complexity of the model and remove unnecessary features. On the other hand, L2 regularization does not make the weights completely 0, but keeps all weights small. L2 regularization is generally more stable and is also called ‘soft regularization’ because it gradually reduces the weights.
L1 and L2 regularizations are applied differently depending on the characteristics of the problem, data, and purpose of the model. While L2 regularization is generally more widely used, it is a good idea to try both and see which one performs better in some cases. Additionally, Elastic Net regularization, which combines L1 and L2 regularization, can also be considered.
Click to view contents (Deep Dive: Elastic Net Regulation - Harmony of L1 and L2)
Elastic Net Regulation - A Combination of L1 and L2
Elastic Net is a regularization method that combines L1 and L2 regulations. By taking the advantages of each regulation and compensating for their disadvantages, it can create more flexible and effective models.
Key Points:
- L1 Regulation (Lasso): Limits the sum of the absolute values of weights. It creates sparse models by making some weights exactly 0. It has a feature selection effect, removing unnecessary features and simplifying the model.
- L2 Regulation (Ridge): Limits the sum of the squares of weights. It prevents overfitting by keeping all weights small. The convergence is stable and smoothly reduces the weights.
- Elastic Net: Applies both L1 and L2 regulations simultaneously. It can achieve the effects of both regulations.
Formula:
The cost function of Elastic Net is expressed as follows:
\(Cost = Loss + \lambda_1 \sum_{i} |w_i| + \lambda_2 \sum_{i} (w_i)^2\)
Loss: The original model’s loss function (e.g., MSE, Cross-Entropy)λ₁: A hyperparameter that controls the strength of L1 regulationλ₂: A hyperparameter that controls the strength of L2 regulationwᵢ: The model’s weights
Advantages:
- Feature Selection + Overfitting Prevention: It can achieve both the feature selection effect of L1 regulation and the overfitting prevention effect of L2 regulation.
- Handling Highly Correlated Features: L1 regulation tends to select only one feature among highly correlated features and set the others to 0. Elastic Net mitigates this issue through L2 regulation, making it tend to select or remove highly correlated features together.
- Flexibility: The weights of L1 and L2 regulations can be adjusted by controlling
λ₁andλ₂. Ifλ₁=0, it becomes L2 regulation (Ridge), and ifλ₂=0, it becomes L1 regulation (Lasso).
Disadvantages:
- Hyperparameter Tuning: It requires tuning two hyperparameters,
λ₁andλ₂, which can be more complex than tuning L1 or L2 regulation. - Computational Cost: Since it calculates both L1 and L2 regulations simultaneously, the computational cost may increase slightly (although this is not a significant issue in modern machine learning).
Applicable Cases:
- When there are many features, and only some of them are expected to be important (feature selection is necessary)
- When there is a high correlation between features
- When it is unclear whether L1 or L2 regulation is better (both can be tried)
- When preventing overfitting while creating a sparse model is desired
Summary: Elastic Net is a powerful regularization method that combines the advantages of L1 and L2 regulations. Although hyperparameter tuning is required, it can perform well in various problems.
6.3 Dropout
6.3.1 Principle of Dropout
Dropout is one of the powerful regularization methods to prevent overfitting in neural networks. During the training process, some neurons are randomly deactivated (dropped out) to prevent specific neurons or combinations of neurons from becoming too dependent on the training data. This has a similar effect to ensemble learning, where multiple people learn different parts and then combine their strengths to solve a problem. Each neuron is encouraged to learn important features independently, improving the model’s generalization performance. It is typically applied to fully connected layers, with a dropout rate of 20% to 50%. Dropout is only applied during training, and all neurons are used during inference.
6.3.2 Implementing Dropout in PyTorch
Dropout can be implemented in PyTorch as follows.
Code
import torch.nn as nn
class Dropout(nn.Module):
def __init__(self, dropout_rate):
super(Dropout, self).__init__()
self.dropout_rate = dropout_rate
def forward(self, x):
if self.training:
mask = torch.bernoulli(torch.ones_like(x) * (1 - self.dropout_rate)) / (1 - self.dropout_rate)
return x * mask
else:
return x
# Usage example. Drops out 0.5 (50%).
dropout = Dropout(dropout_rate=0.5)
# Example input data
inputs = torch.randn(1000, 100)
# Forward pass (during training)
dropout.train()
outputs_train = dropout(inputs)
# Forward pass (during inference)
dropout.eval()
outputs_test = dropout(inputs)
print("Input shape:", inputs.shape)
print("Training output shape:", outputs_train.shape)
print("Test output shape", outputs_test.shape)
print("Dropout rate (should be close to 0.5):", 1 - torch.count_nonzero(outputs_train) / outputs_train.numel())Input shape: torch.Size([1000, 100])
Training output shape: torch.Size([1000, 100])
Test output shape torch.Size([1000, 100])
Dropout rate (should be close to 0.5): tensor(0.4997)The implementation is very simple. It multiplies the mask value to the input tensor and inactivates a certain percentage of neurons. The dropout layer does not have separate learnable parameters, but simply plays the role of randomly making some of the inputs 0. In actual neural networks, the dropout layer is used by inserting it between other layers (e.g., linear layers, convolutional layers).
Dropout removes neurons randomly during training, but uses all neurons during inference. To match the scale of output values between training and inference, the inverted dropout method is used. Inverted dropout performs scaling in advance by dividing by (1 - dropout_rate) during training, so that it can be used as is without additional calculations during inference. This allows achieving an effect similar to ensemble learning during inference, i.e., averaging multiple sub-networks, while also improving computational efficiency.
Let’s take a look at how effective dropout is through a graph using simple data. The source code is chapter_06/plot_dropout.py, and we will omit introducing the unimportant code due to space constraints. Since it has detailed comments, it’s not difficult to look at the source code. When drawing the graph, we can see that the model with dropout applied (blue) has a much higher test accuracy.
Code
from dldna.chapter_06.plot_dropout import plot_dropout_effect
plot_dropout_effect()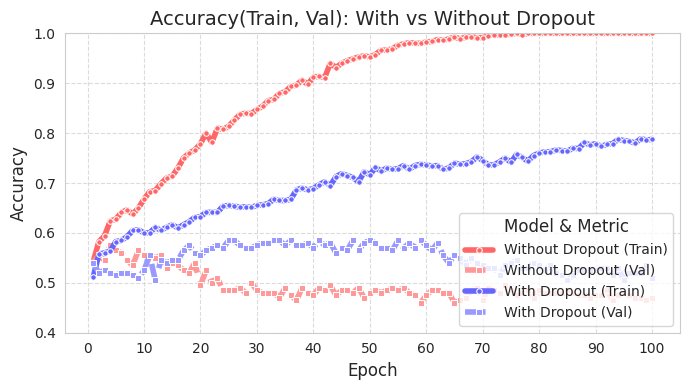
The training accuracy of the model with dropout (With Dropout) is lower than that of the model without dropout (Without Dropout), but the validation accuracy is higher. This means that dropout reduces overfitting to the training data and improves the generalization performance of the model.
6.4 Batch Normalization
6.4.1 Concept and Effect of Batch Normalization
Batch normalization plays a role in regularization and also increases the stability of data during training. Batch normalization was first proposed in the 2015 paper by Ioffe and Szegedy [Reference 2]. In deep learning, as data passes through each layer, the distribution of activation values changes, causing an internal covariate shift. This slows down the training speed and makes the model unstable (since the distribution changes, more calculation steps are required). This problem becomes more severe as the number of layers increases. Batch normalization mitigates this by normalizing the data in mini-batch units.
The core idea of batch normalization is to normalize the data in mini-batch units. The following code illustrates this easily.
Code
# Calculate the mean and variance of the mini-batch
batch_mean = x.mean(dim=0)
batch_var = x.var(dim=0, unbiased=False)
# Perform normalization
x_norm = (x - batch_mean) / torch.sqrt(batch_var + epsilon)
# Apply scale and shift parameters
y = gamma * x_norm + betaGenerally, batch normalization uses the variance and mean of the data within a single mini-batch to normalize the entire data, bringing about distributional changes. It first performs normalization, then applies a certain scale parameter and shift parameter. The gamma above is the scale parameter, and beta is the shift parameter. It’s helpful to think of it simply as \(y = ax + b\). The epsilon used during normalization is a very small constant value (1e-5 or 1e-7) that often appears in numerical analysis, and is used for numerical stability. Batch normalization provides the following additional effects:
- Improved learning speed: By stabilizing the distribution of activation values for each layer, it alleviates the gradient vanishing/exploding problem, allowing the use of larger learning rates.
- Reduced dependence on initialization: It makes the model less sensitive to weight initialization, making it easier to start training.
- Regularization effect: Since statistics are calculated for each mini-batch, it has the effect of adding a bit of noise, which helps prevent overfitting. (Using it with dropout is even more effective.)
Let’s compare the case where pure normalization is applied to randomly generated data with two features, and the case where scale and shift parameters are applied, using a graph. Through visualization, we can easily understand the numerical meaning of normalization for mini-batches.
Code
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# Generate data
np.random.seed(42)
x = np.random.rand(50, 2) * 10
# Batch normalization (including scaling parameters)
def batch_normalize(x, epsilon=1e-5, gamma=1.0, beta=0.0):
mean = x.mean(axis=0)
var = x.var(axis=0)
x_norm = (x - mean) / np.sqrt(var + epsilon)
x_scaled = gamma * x_norm + beta
return x_norm, mean, x_scaled
# Perform normalization (gamma=1.0, beta=0.0 is pure normalization)
x_norm, mean, x_norm_scaled = batch_normalize(x, gamma=1.0, beta=0.0)
# Perform normalization and scaling (apply gamma=2.0, beta=1.0)
_, _, x_scaled = batch_normalize(x, gamma=2.0, beta=1.0)
# Set Seaborn style
sns.set_style("whitegrid")
sns.set_context("notebook", font_scale=1.2)
# Visualization
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))
# Original data
sns.scatterplot(x=x[:, 0], y=x[:, 1], ax=ax1, color='royalblue', alpha=0.7)
ax1.scatter(mean[0], mean[1], color='red', marker='*', s=200, label='Mean')
ax1.set(title='Original Data',
xlabel='Feature 1',
ylabel='Feature 2',
xlim=(-2, 12),
ylim=(-2, 12))
ax1.legend()
# After normalization (gamma=1, beta=0)
sns.scatterplot(x=x_norm[:, 0], y=x_norm[:, 1], ax=ax2, color='crimson', alpha=0.7)
ax2.scatter(0, 0, color='blue', marker='*', s=200, label='Mean (0,0)')
ax2.axhline(y=0, color='k', linestyle='--', alpha=0.3)
ax2.axvline(x=0, color='k', linestyle='--', alpha=0.3)
ax2.set(title='After Normalization (γ=1, β=0)',
xlabel='Normalized Feature 1',
ylabel='Normalized Feature 2',
xlim=(-2, 12),
ylim=(-2, 12))
ax2.legend()
# After scaling and shifting (gamma=2, beta=1)
sns.scatterplot(x=x_scaled[:, 0], y=x_scaled[:, 1], ax=ax3, color='green', alpha=0.7)
ax3.scatter(1, 1, color='purple', marker='*', s=200, label='New Mean')
ax3.axhline(y=1, color='k', linestyle='--', alpha=0.3)
ax3.axvline(x=1, color='k', linestyle='--', alpha=0.3)
ax3.set(title='After Scale & Shift (γ=2, β=1)',
xlabel='Scaled Feature 1',
ylabel='Scaled Feature 2',
xlim=(-2, 12),
ylim=(-2, 12))
ax3.legend()
plt.tight_layout()
plt.show()
# Print statistics
print("\nOriginal Data Statistics:")
print(f"Mean: {mean}")
print(f"Variance: {x.var(axis=0)}")
print("\nNormalized Data Statistics (γ=1, β=0):")
print(f"Mean: {x_norm.mean(axis=0)}")
print(f"Variance: {x_norm.var(axis=0)}")
print("\nScaled Data Statistics (γ=2, β=1):")
print(f"Mean: {x_scaled.mean(axis=0)}")
print(f"Variance: {x_scaled.var(axis=0)}")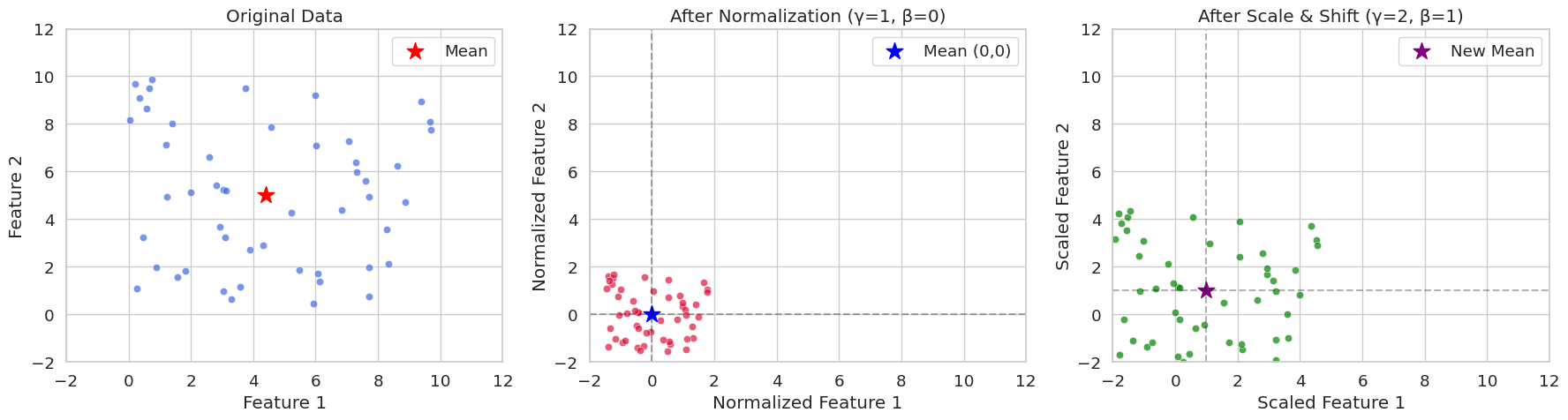
Original Data Statistics:
Mean: [4.40716778 4.99644709]
Variance: [8.89458134 8.45478364]
Normalized Data Statistics (γ=1, β=0):
Mean: [-2.70894418e-16 -3.59712260e-16]
Variance: [0.99999888 0.99999882]
Scaled Data Statistics (γ=2, β=1):
Mean: [1. 1.]
Variance: [3.9999955 3.99999527]In seed(42), you can often see that the random initial value is set to 42. This is a programmer’s habit, and other numbers can also be used. 42 is a number that appears in Douglas Adams’ novel “The Hitchhiker’s Guide to the Galaxy” as the “answer to life, the universe, and everything”. Therefore, it is often used as an example code among programmers.
6.4.2 Batch Normalization Implementation in PyTorch
In PyTorch, the implementation typically involves inserting batch normalization layers into neural network layers. The following is an example.
Code
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self):
super().__init__()
self.network = nn.Sequential(
nn.Linear(784, 256),
nn.BatchNorm1d(256), # 배치 정규화 층
nn.ReLU(),
nn.Linear(256, 10)
)
def forward(self, x):
return self.network(x)PyTorch batch normalization implementation based on the original source code can be simplified as follows, and as done in the previous chapter, it is implemented briefly for learning purposes.
Code
import torch
import torch.nn as nn
class BatchNorm1d(nn.Module):
def __init__(self, num_features, eps=1e-5, momentum=0.1):
super().__init__()
self.num_features = num_features
self.eps = eps
self.momentum = momentum
# Trainable parameters
self.gamma = nn.Parameter(torch.ones(num_features)) # scale
self.beta = nn.Parameter(torch.zeros(num_features)) # shift
# Running statistics to be tracked
self.register_buffer('running_mean', torch.zeros(num_features))
self.register_buffer('running_var', torch.ones(num_features))
def forward(self, x):
if self.training:
# Calculate mini-batch statistics
batch_mean = x.mean(dim=0) # Mean per channel
batch_var = x.var(dim=0, unbiased=False) # Variance per channel
# Update running statistics (important)
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var
# Normalize
x_norm = (x - batch_mean) / torch.sqrt(batch_var + self.eps)
else:
# During inference, use the stored statistics
x_norm = (x - self.running_mean) / torch.sqrt(self.running_var + self.eps)
# Apply scale and shift
return self.gamma * x_norm + self.betaThe biggest difference from the basic implementation is the part that updates statistics during execution. During training, it allows you to finally know the overall average and variance by accumulating the statistical values (average and variance) of the mini-batch as it moves. To track the movement, an exponential moving average (Exponential Moving Average) using momentum (default 0.1) is used. By using the average and variance obtained during training for inference, accurate variance and deviation are applied to the inference data, ensuring consistency between learning and inference.
Of course, this implementation is highly simplified for learning purposes. The location of the reference code is (https://github.com/pytorch/pytorch/blob/main/torch/nn/modules/batchnorm.py). The actual implementation of BatchNorm1d is much more complex. This is because frameworks such as PyTorch and TensorFlow typically include various logic beyond basic logic, including CUDA optimization, gradient optimization, handling various settings, and linking with C/C++.
Click to view contents (Deep Dive: Derivation of Batch Normalization Formula and Detailed Analysis of Backpropagation Process)
Derivation of Batch Normalization Formula and Detailed Analysis of Backpropagation Process
Batch normalization (BN), proposed by Ioffe & Szegedy in 2015, has become a key technique in deep learning model training. BN accelerates the learning speed by normalizing the input of each layer, alleviates the vanishing/exploding gradient problem, and provides some regularization effect. In this deep dive, we will examine the forward and backward pass processes of BN in detail and analyze its effects mathematically.
Derivation of Batch Normalization Forward Pass Formula
Batch normalization is performed on a mini-batch basis. Given a mini-batch size of \(B\) and a feature dimension of \(D\), the mini-batch input data can be represented as a \(B \times D\) matrix \(\mathbf{X}\). Since BN operates independently for each feature dimension, we will consider only one feature dimension for explanation.
Mini-Batch Mean Calculation:
\(\mu_B = \frac{1}{B} \sum_{i=1}^{B} x_i\)
Here, \(x_i\) represents the value of the corresponding feature for the \(i\)th sample in the mini-batch.
Mini-Batch Variance Calculation:
\(\sigma_B^2 = \frac{1}{B} \sum_{i=1}^{B} (x_i - \mu_B)^2\)
Normalization:
\(\hat{x_i} = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\)
Here, \(\epsilon\) is a small constant to prevent the denominator from being zero.
Scaling and Shifting:
\(y_i = \gamma \hat{x_i} + \beta\)
Here, \(\gamma\) and \(\beta\) are learnable parameters responsible for scaling and shifting, respectively. These parameters restore the representation power of the normalized data.
Derivation of Batch Normalization Backward Pass Formula - Including Computational Graph
The backward pass of batch normalization involves calculating the gradients of the loss function with respect to each parameter using the chain rule. The process can be visually represented through a computational graph as follows (simplified using ASCII art):
x_i --> [-] --> [/] --> [*] --> [+] --> y_i
| ^ ^ ^ ^
| | | | |
| | | | +---> beta
| | | +---> gamma
| | +---> sqrt(...) + epsilon
| +---> mu_B, sigma_B^2- \(x_i\): input
- \([-]\): subtraction (\(x_i - \mu_B\))
- \([/]\): division (\((x_i - \mu_B) / \sqrt{\sigma_B^2 + \epsilon}\))
- \([*]\): multiplication (\(\gamma \hat{x_i}\))
- \([+]\): addition (\(\gamma \hat{x_i} + \beta\))
- \(y_i\): output
- \(\mu_B\): mean
- \(\sigma_B^2\): variance
- \(\epsilon\): small number to prevent division by zero
- \(\gamma, \beta\): learnable parameters Now, let’s calculate the backpropagation for each step. Let the loss function be \(\mathcal{L}\) and assume that \(\frac{\partial \mathcal{L}}{\partial y_i}\) is given.
Calculation of \(\frac{\partial \mathcal{L}}{\partial \beta}\) and \(\frac{\partial \mathcal{L}}{\partial \gamma}\):
\(\frac{\partial \mathcal{L}}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i}\)
\(\frac{\partial \mathcal{L}}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \hat{x_i}\)
Calculation of \(\frac{\partial \mathcal{L}}{\partial \hat{x_i}}\):
\(\frac{\partial \mathcal{L}}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \gamma\)
Calculation of \(\frac{\partial \mathcal{L}}{\partial \sigma_B^2}\):
\(\frac{\partial \mathcal{L}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot (x_i - \mu_B) \cdot (-\frac{1}{2})(\sigma_B^2 + \epsilon)^{-3/2}\)
Calculation of \(\frac{\partial \mathcal{L}}{\partial \mu_B}\):
\(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \mu_B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot (-2)\frac{1}{B}\sum_{i=1}^B (x_i-\mu_B)\)
Since \(\sum_{i=1}^B (x_i - \mu_B) = 0\) \(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}}\)
\(\frac{\partial \mathcal{L}}{\partial x_i}\) calculation:
\(\frac{\partial \mathcal{L}}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{\partial \mu_B}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{1}{B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{2}{B}(x_i - \mu_B)\)
Principle of Batch Normalization Alleviating Gradient Vanishing/Exploding Problems
Batch normalization prevents the input of each layer from becoming extremely large or small by normalizing it, which helps alleviate the gradient vanishing/exploding problems that occur in activation functions such as sigmoid or tanh.
- Gradient Vanishing Problem: When the input of an activation function becomes very large or small, its gradient approaches 0, causing the gradient to disappear during backpropagation. Batch normalization alleviates this problem by normalizing the input to have a mean of 0 and a variance of 1, keeping the input within an appropriate range.
- Gradient Exploding Problem: When the input of an activation function becomes very large, its gradient becomes extremely large. Batch normalization limits the range of inputs, thereby alleviating the gradient exploding problem.
Calculation and Inference of Running Mean and Running Variance in Batch Normalization
During training, batch normalization calculates the mean and variance for each mini-batch, but during inference, it requires an estimate of the mean and variance of the entire training data. To achieve this, batch normalization calculates the running mean and running variance during training.
Running Mean Calculation:
\(\text{running\_mean} = (1 - \text{momentum}) \times \text{running\_mean} + \text{momentum} \times \mu_B\)
Running Variance Calculation:
\(\text{running\_var} = (1 - \text{momentum}) \times \text{running\_var} + \text{momentum} \times \sigma_B^2\)
Here, momentum is a hyperparameter that is typically set to a small value such as 0.1 or 0.01.
During inference, the running_mean and running_var calculated during training are used to normalize the input.
Comparison of Batch Normalization with Other Normalization Techniques (Layer Normalization, Instance Normalization, Group Normalization)
Batch Normalization (BN): uses statistics from within the mini-batch of samples. It is affected by batch size and is difficult to apply to RNNs.
Layer Normalization (LN): uses statistics from within each sample over the feature dimension. It is not affected by batch size and is easy to apply to RNNs.
Instance Normalization (IN): calculates statistics independently for each sample and each channel. It is mainly used in image generation tasks such as style transfer.
Group Normalization (GN): divides channels into groups and calculates statistics within each group. It can be used as an alternative to BN when the batch size is small.
Each normalization technique has its own strengths and weaknesses under different circumstances, so it’s necessary to choose the right technique according to the characteristics of the problem and model architecture.
6.4.3 Statistical Tracking and Inference Application
6.5 Hyperparameter Optimization
Hyperparameter optimization has a significant impact on model performance. Its importance began to be recognized in the 1990s. In the late 1990s, it was discovered in Support Vector Machines (SVM) that even with the same model, the parameters of the kernel function (C, gamma, etc.) played a crucial role in performance. Around 2015, it was proven that Bayesian optimization yields better results than manual tuning, which became the core foundation for automated tuning methods like Google AutoML (2017).
6.5.1 Comparison of Optimization Methodologies
There are several methods to optimize hyperparameters. The representative methods are as follows:
Grid Search: The most basic method, where possible values for each hyperparameter are listed and all combinations of these values are tried. It is useful when the number of hyperparameters is small and the range of values each parameter can take is limited, but it incurs high computational costs because all combinations must be tested. It is suitable for testing simple models or when the search space is very small.
Random Search: Hyperparameter values are randomly selected to create combinations, and these combinations are used to train the model and evaluate its performance. If some hyperparameters have a significant impact on performance, it can be more effective than grid search (Bergstra & Bengio, 2012).
Bayesian Optimization: Based on previous search results, a probabilistic model (usually Gaussian process) is used to intelligently select the next hyperparameter combination to try. It selects the next exploration point by maximizing an acquisition function. By efficiently exploring the hyperparameter search space, it can find better combinations with fewer trials than grid search or random search.
There are also other methods such as evolutionary algorithms using genetic algorithms and gradient-based optimization.
The following is an example of optimizing hyperparameters for a simple neural network model using Bayesian optimization.
6.5.2 Optimization Using Bayes-Opt
Bayesian optimization began to gain attention in the 2010s. Especially after the publication of the paper “Practical Bayesian Optimization of Machine Learning Algorithms” in 2012, it has become one of the main methods for optimizing hyperparameters of deep learning models. Unlike grid search or random search, its significant advantage is that it intelligently selects the next parameter to explore based on previous trial results.
Bayesian optimization largely repeats the following three steps:
- Initialization: Randomly select hyperparameter combinations and train the model to evaluate its performance for the number of times specified by
init_points. - Surrogate Model Construction: Based on the experimental results so far, construct a surrogate model (usually a Gaussian process) that models the relationship between hyperparameters and performance.
- Acquisition Function Optimization: Based on the surrogate model, select the most promising hyperparameter combination to try next. At this time, an acquisition function is used, which determines the next exploration point by balancing “exploration” and “exploitation” based on the current information (surrogate model).
- Repeat steps 2-3
Code
import torch
import torch.nn as nn
import torch.optim as optim
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from bayes_opt import BayesianOptimization
from dldna.chapter_04.experiments.model_training import train_model, eval_loop
def train_simple_net(hidden_layers, learning_rate, batch_size, epochs):
"""Trains a SimpleNetwork model with given hyperparameters.
Uses CIFAR100 dataset and train_model from Chapter 4.
"""
device = get_device() # Use the utility function to get device
# Get data loaders for CIFAR100
train_loader, test_loader = get_data_loaders(dataset="CIFAR100", batch_size=batch_size)
# Instantiate the model with specified activation and hidden layers.
# CIFAR100 images are 3x32x32, so the input size is 3*32*32 = 3072.
model = SimpleNetwork(act_func=nn.ReLU(), input_shape=3*32*32, hidden_shape=hidden_layers, num_labels=100).to(device)
# Optimizer: Use Adam
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# Train the model using the training function from Chapter 4
results = train_model(model, train_loader, test_loader, device, optimizer=optimizer, epochs=epochs, save_dir="./tmp/tune",
retrain=True) # retrain=True로 설정
# Return the final test accuracy
return results['test_accuracies'][-1]
def train_wrapper(learning_rate, batch_size, hidden1, hidden2):
"""Wrapper function for Bayesian optimization."""
return train_simple_net(
hidden_layers=[int(hidden1), int(hidden2)],
learning_rate=learning_rate,
batch_size=int(batch_size),
epochs=10
)
def optimize_hyperparameters():
"""Runs hyperparameter optimization."""
# Set the parameter ranges to be optimized.
pbounds = {
"learning_rate": (1e-4, 1e-2),
"batch_size": (64, 256),
"hidden1": (64, 512), # First hidden layer
"hidden2": (32, 256) # Second hidden layer
}
# Create a Bayesian optimization object.
optimizer = BayesianOptimization(
f=train_wrapper,
pbounds=pbounds,
random_state=1,
allow_duplicate_points=True
)
# Run optimization
optimizer.maximize(
init_points=4,
n_iter=10,
)
# Print the best parameters and accuracy
print("\nBest parameters found:")
print(f"Learning Rate: {optimizer.max['params']['learning_rate']:.6f}")
print(f"Batch Size: {int(optimizer.max['params']['batch_size'])}")
print(f"Hidden Layer 1: {int(optimizer.max['params']['hidden1'])}")
print(f"Hidden Layer 2: {int(optimizer.max['params']['hidden2'])}")
print(f"\nBest accuracy: {optimizer.max['target']:.4f}")
if __name__ == "__main__":
print("Starting hyperparameter optimization...")
optimize_hyperparameters()The above example performs hyperparameter optimization using the BayesOpt package. The SimpleNetwork (defined in Chapter 4) is used as the training target, and the CIFAR100 dataset is used. The train_wrapper function serves as the objective function for BayesOpt, training the model with a given combination of hyperparameters and returning the final test accuracy.
pbounds specifies the search range for each hyperparameter. In optimizer.maximize, init_points is the number of initial random searches, and n_iter is the number of Bayesian optimization iterations. Therefore, the total number of experiments is init_points + n_iter.
When searching for hyperparameters, note the following:
- Parameter range: A range that is too wide increases the search time, while a range that is too narrow may miss the optimal point. Typically, the learning rate is set on a log scale (1e-4 ~ 1e-2), and the number of neurons is set in units of powers of 2.
- Number of iterations: The total number of attempts is roughly set to (number of parameters) x 20, which empirically gives good results. In the above example, there are 4 parameters, so a total of 14 attempts (init_points=4, n_iter=10) may be slightly insufficient. To get better results, consider increasing
n_iter.
6.5.3 Optimization using BoTorch
The BoTorch framework has recently gained attention in the field of deep learning hyperparameter optimization. BoTorch is a Bayesian optimization framework based on PyTorch, developed by FAIR (Facebook AI Research, now Meta AI) in 2019. Bayes-Opt is an older Bayesian optimization library that has been developed since 2016 and provides an intuitive and simple interface (scikit-learn style API), making it widely used.
The advantages and disadvantages of the two libraries are clear.
- BoTorch:
- Advantages: Provides features specialized for deep learning model hyperparameter optimization, such as integration with deep learning models, GPU acceleration, high sampling efficiency, various advanced Bayesian optimization techniques (multi-fidelity, multi-task, constrained optimization, etc.), and automatic differentiation support. It is particularly suitable for large-scale models, high-dimensional parameter spaces, and experiments with high computational costs.
- Disadvantages: Requires relatively more learning compared to Bayes-Opt, and the initial setup can be complex.
- Bayes-Opt:
- Advantages: Provides a simple and intuitive API, making it easy to use. Installation is straightforward, and there are many tutorials and example codes available.
- Disadvantages: Lacks advanced features compared to BoTorch, and integration with deep learning models is relatively less smooth. Performance may degrade for large-scale/high-dimensional problems.
Therefore, Bayes-Opt is suitable for simple problems or rapid prototyping, while BoTorch is recommended for complex hyperparameter optimization of deep learning models, large-scale/high-dimensional problems, or advanced Bayesian optimization techniques (e.g., multi-task, constrained optimization).
To use BoTorch, unlike Bayes-Opt, you need to understand a few key concepts required for initial setup: surrogate models, input data normalization, and acquisition functions.
Surrogate Model:
A surrogate model is a model that approximates the actual objective function (in this case, the validation accuracy of a deep learning model). Typically, a Gaussian process (GP) is used. GP is used to predict results quickly and cheaply instead of the actual objective function, which can be computationally expensive. BoTorch provides the following GP models:
SingleTaskGP: The most basic Gaussian process model, suitable for single-objective optimization problems and effective with relatively small datasets (less than 1000 data points).MultiTaskGP: Used for multi-objective optimization problems where multiple objective functions are optimized simultaneously. For example, you can optimize both the accuracy and inference time of a model.SAASBO(Sparsity-Aware Adaptive Subspace Bayesian Optimization): A model specialized for high-dimensional parameter spaces. It assumes sparsity in high-dimensional spaces and performs efficient exploration.
Input Data Normalization:
Gaussian processes are sensitive to the scale of the data, so normalizing the input data (hyperparameters) is crucial. Typically, all hyperparameters are transformed to the range [0, 1]. BoTorch provides
NormalizeandStandardizetransformations.Acquisition Function:
The acquisition function determines the next point to evaluate based on the current surrogate model. It balances exploration (searching for new areas) and exploitation (focusing on areas with high predicted performance). Common acquisition functions include probability of improvement (PI), expected improvement (EI), and Thompson sampling. BoTorch provides a variety of acquisition functions, including
ProbabilityOfImprovement,ExpectedImprovement, andUpperConfidenceBound. The acquisition function is based on a surrogate model (GP) and is used to determine the next hyperparameter combination to experiment with. The acquisition function balances the trade-off between “exploration” and “exploitation”. BoTorch provides the following various acquisition functions.
ExpectedImprovement (EI): One of the most common acquisition functions, considering both the probability of getting a better result than the current optimum and the magnitude of improvement.LogExpectedImprovement (LogEI): A log-transformed version of EI, which is numerically more stable and sensitive to small changes.UpperConfidenceBound (UCB): An acquisition function that focuses more on exploration, actively exploring areas with high uncertainty.ProbabilityOfImprovement (PI): Represents the probability of improvement over the current optimum.qExpectedImprovement (qEI): Also known as q-batch EI, used for parallel optimization, selecting multiple candidates at once.qNoisyExpectedImprovement (qNEI): Q-batch Noisy EI, used in noisy environments.
The entire code is located in package/botorch_optimization.py and can be run directly from the command line. Since the full code contains detailed comments, we will only explain the important parts here.
Code
def __init__(self, max_trials: int = 80, init_samples: int = 10):
self.param_bounds = torch.tensor([
[1e-4, 64.0, 32.0, 32.0], # 최소값
[1e-2, 256.0, 512.0, 512.0] # 최대값
], dtype=torch.float64)In the initialization part, the minimum and maximum values of each hyperparameter are set. max_trials is the total number of attempts, and init_samples is the initial number of random experiments (same as init_points in Bayes-Opt). init_samples is typically set to 2-3 times the number of parameters. In the above example, since there are 4 hyperparameters, around 8-12 would be suitable. torch.float64 is used for numerical stability. Bayesian optimization, especially Gaussian process, uses Cholesky decomposition when calculating kernel matrices, and in this process, float32 can cause errors due to precision issues.
Code
def tune(self):
# 가우시안 프로세스 모델 학습
model = SingleTaskGP(configs, accuracies)
mll = ExactMarginalLogLikelihood(model.likelihood, model)
fit_gpytorch_mll(mll)We use SingleTaskGP as a surrogate model based on Gaussian processes. ExactMarginalLogLikelihood is the loss function for model training, and fit_gpytorch_mll trains the model using this loss function.
Code
acq_func = LogExpectedImprovement(
model,
best_f=accuracies.max().item()
)The acquisition function used is LogExpectedImprovement. It uses a log, so it has high numerical stability and is sensitive to small changes.
Code
candidate, _ = optimize_acqf( # 획득 함수 최적화로 다음 실험할 파라미터 선택
acq_func, bounds=bounds, # 획득 함수와 파라미터 범위 지정
q=1, # 한 번에 하나의 설정만 선택
num_restarts=10, # 최적화 재시작 횟수
raw_samples=512 # 초기 샘플링 수
)The optimize_acqf function optimizes the acquisition function to select the next hyperparameter combination (candidate) for experimentation.
q=1: Selects one candidate at a time (not q-batch optimization).num_restarts=10: Performs each optimization step 10 times with different starting points to prevent getting stuck in local optima.raw_samples=512: Draws 512 samples from the Gaussian process to estimate the acquisition function value.
num_restarts and raw_samples significantly impact the exploration-exploitation trade-off in Bayesian optimization. num_restarts determines the thoroughness of the optimization, while raw_samples determines the accuracy of the acquisition function estimation. Larger values increase computational cost but provide a higher chance of better results. The following values can be used:
- Fast execution:
num_restarts=5,raw_samples=256 - Balanced setting:
num_restarts=10,raw_samples=512 - Accuracy-focused:
num_restarts=20,raw_samples=1024
Code
from dldna.chapter_06.botorch_optimizer import run_botorch_optimization
run_botorch_optimization(max_trials=80, init_samples=5)Results Dataset: FashionMNIST Epochs: 20 Initial experiments: 5 times Repeated experiments: 80 times
| Optimal parameters | Bayes-Opt | Botorch |
|---|---|---|
| Learning rate | 6e-4 | 1e-4 |
| Batch size | 173 | 158 |
| hid 1 | 426 | 512 |
| hid 2 | 197 | 512 |
| Accuracy | 0.7837 | 0.8057 |
Although this is a simple comparison, Botorch’s accuracy is higher. For simple parameter tuning, Bayes-Opt is recommended, while for professional tuning, Botorch is recommended.
6.6 Gaussian Process
Challenge: What methods can quantify the predictive uncertainty of a model and utilize it for active learning?
Researcher’s Concern: Traditional deep learning models provide point estimates as predictions, but in real-world applications, knowing the uncertainty of predictions is crucial. For example, an autonomous vehicle needs to know how uncertain its prediction of a pedestrian’s next location is to drive safely. Gaussian processes were powerful tools for quantifying predictive uncertainty based on Bayesian probability, but they had limitations such as high computational complexity and difficulty in applying them to large-scale data.
Gaussian Process (GP) is a core model in Bayesian machine learning that provides predictions with uncertainty. Previously, we briefly looked at using Gaussian processes as surrogate models in Bayesian optimization; here, we will delve deeper into the basic principles and importance of Gaussian processes themselves.
GP is defined as a “probability distribution over a set of function values.” Unlike deterministic functions like \(y = f(x)\), GP does not predict a single output value \(y\) for a given input \(x\), but instead predicts a distribution of possible output values. For instance, instead of predicting “tomorrow’s high temperature will be 25 degrees” deterministically, it predicts “there is a 95% chance that tomorrow’s high temperature will be between 23 and 27 degrees,” providing uncertainty along with the prediction. If you are riding a bike back home, the general route is already determined, but the actual route will vary each time. This requires predictions that include uncertainty rather than deterministic ones.
The mathematical basis for tools that handle predictions with uncertainty is the normal distribution (Gaussian distribution) proposed by the 19th-century mathematician Gauss. Based on this, GP developed in the 1940s. At that time, during World War II, scientists had to deal with more uncertain data than ever before, such as radar signal processing, code decryption, and weather information processing. A notable example is Norbert Wiener’s effort to improve anti-aircraft gun accuracy by predicting the future position of an aircraft. He conceived the “Wiener process,” which views the movement of an airplane as a stochastic process (current location - predictable to some extent after a while - increasing uncertainty over time), laying important groundwork for GP. Around the same period, Harald Cramér was working on the mathematical foundations of GP in time series analysis, and Andrey Kolmogorov in probability theory. In 1951, Daniel Krige created a practical application of GP for predicting ore distributions. Subsequently, in the 1970s, statisticians systematized GP for applications in spatial statistics, computer experimental design, and Bayesian optimization in ML. Today, GP plays a core role in almost every field that deals with uncertainty, including AI, robotics, climate prediction, and more. Especially in deep learning, deep kernel GP through meta-learning has recently gained attention and shows excellent performance, particularly in fields like molecular property prediction.
Today, GP is being utilized in various fields such as AI, robotics, climate modeling, and more. Especially in deep learning, recent advancements in meta-learning through deep kernel GP and applications like molecular property prediction have shown outstanding performance.
Click to view contents (Deep Dive: Mathematical Foundations of Gaussian Processes and Machine Learning Applications)
Mathematical Foundations of Gaussian Processes and Machine Learning Applications
Gaussian Process (GP) is a probabilistic model based on kernel methods, widely used for regression and classification problems. GP has the advantage of defining a distribution over functions themselves, allowing for quantification of prediction uncertainty. In this deep dive, we explore the mathematical foundations of Gaussian Processes from multivariate normal distributions to stochastic processes, and delve into various machine learning applications.
1. Multivariate Normal Distribution
The first step in understanding Gaussian Processes is understanding multivariate normal distributions. A \(d\)-dimensional random vector \(\mathbf{x} = (x_1, x_2, ..., x_d)^T\) following a multivariate normal distribution means it has the following probability density function:
\(p(\mathbf{x}) = \frac{1}{(2\pi)^{d/2}|\mathbf{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)\)
where \(\boldsymbol{\mu} \in \mathbb{R}^d\) is the mean vector and \(\mathbf{\Sigma} \in \mathbb{R}^{d \times d}\) is the covariance matrix. The covariance matrix must be a positive definite matrix.
Key Properties:
Linear Transformation: A linear transformation of a random variable following a multivariate normal distribution still follows a multivariate normal distribution. That is, if \(\mathbf{x} \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{\Sigma})\) and \(\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{b}\), then \(\mathbf{y} \sim \mathcal{N}(\mathbf{A}\boldsymbol{\mu} + \mathbf{b}, \mathbf{A}\mathbf{\Sigma}\mathbf{A}^T)\).
Conditional Distribution: The conditional distribution of a multivariate normal distribution is also normal. By partitioning \(\mathbf{x}\) into \(\mathbf{x} = (\mathbf{x}_1, \mathbf{x}_2)^T\) and similarly partitioning the mean and covariance matrix:
\(\boldsymbol{\mu} = \begin{pmatrix} \boldsymbol{\mu}_1 \\ \boldsymbol{\mu}_2 \end{pmatrix}, \quad \mathbf{\Sigma} = \begin{pmatrix} \mathbf{\Sigma}_{11} & \mathbf{\Sigma}_{12} \\ \mathbf{\Sigma}_{21} & \mathbf{\Sigma}_{22} \end{pmatrix}\)
The conditional distribution of \(\mathbf{x}_2\) given \(\mathbf{x}_1\) is:
\(p(\mathbf{x}_2 | \mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu}_{2|1}, \mathbf{\Sigma}_{2|1})\)
\(\boldsymbol{\mu}_{2|1} = \boldsymbol{\mu}_2 + \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}(\mathbf{x}_1 - \boldsymbol{\mu}_1)\) \(\mathbf{\Sigma}_{2|1} = \mathbf{\Sigma}_{22} - \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}\mathbf{\Sigma}_{12}\)
Marginal Distribution: The marginal distribution of a multivariate normal distribution is also a normal distribution. In the partition above, the marginal distribution of \(\mathbf{x}_1\) is as follows. \(p(\mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu_1}, \mathbf{\Sigma}_{11})\)
2. Definition and Interpretation of Gaussian Process
A Gaussian process is a probability distribution over functions. That is, if some function \(f(x)\) follows a Gaussian process, it means that the vector of function values at any finite set of input points \(\{x_1, x_2, ..., x_n\}\), \((f(x_1), f(x_2), ..., f(x_n))^T\), follows a multivariate normal distribution.
Definition: A Gaussian process is defined by a mean function \(m(x)\) and a covariance function (or kernel function) \(k(x, x')\).
\(f(x) \sim \mathcal{GP}(m(x), k(x, x'))\)
- Mean Function: \(m(x) = \mathbb{E}[f(x)]\)
- Covariance Function: \(k(x, x') = \mathbb{E}[(f(x) - m(x))(f(x') - m(x'))]\)
Stochastic Process Perspective: A Gaussian process is a type of stochastic process that assigns a random variable to each element in the index set (here, the input space). In a Gaussian process, these random variables form a joint Gaussian distribution.
3. Role and Introduction of Kernel Function
The kernel function is one of the most important elements in a Gaussian process. The kernel function represents the similarity between two inputs \(x\) and \(x'\) and determines the properties of the Gaussian process.
Key Roles:
- Covariance Definition: The kernel function defines the covariance between function values. That is, \(k(x, x')\) represents the covariance between \(f(x)\) and \(f(x')\).
- Function Smoothness Determination: The kernel function determines the smoothness of the generated function. For example, the RBF kernel generates infinitely differentiable functions, while the Matern kernel can adjust differentiability.
- Positive Definiteness: To be a valid covariance function, the kernel function must satisfy positive definiteness. That is, for any input points, the resulting kernel matrix (Gram matrix) must be a positive definite matrix.
Various Kernel Functions:
RBF (Radial Basis Function) Kernel (or Squared Exponential Kernel):
\(k(x, x') = \sigma^2 \exp\left(-\frac{\|x - x'\|^2}{2l^2}\right)\)
- \(\sigma^2\): variance
- \(l\): length scale
- Generates very smooth functions.
Matern Kernel:
\(k(x, x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)}\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)^\nu K_\nu\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)\)
\(\nu\): smoothness parameter
\(K_\nu\): modified Bessel function
\(\nu = 1/2, 3/2, 5/2\) and other half-integer values are commonly used.
As \(\nu\) increases, it approaches the RBF kernel.
Periodic kernel:
\(k(x, x') = \sigma^2 \exp\left(-\frac{2\sin^2(\pi|x-x'|/p)}{l^2}\right)\)
- \(p\): period
Linear kernel:
\(k(x,x') = \sigma_b^2 + \sigma_v^2(x - c)(x' -c)\)
4. Solving Regression and Classification Problems using Gaussian Processes
Regression:
Gaussian process regression is the problem of predicting the output \(f(\mathbf{x}_*)\) for a new input \(\mathbf{x}_*\) given the training data \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n\). The prior distribution of the Gaussian process and the training data are combined to compute the posterior distribution, which is then used to obtain the predictive distribution.
- Prior distribution: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\) (assuming the mean function is 0 for simplicity)
- Training data: \(\mathbf{y} = (y_1, y_2, ..., y_n)^T\)
- Kernel matrix: \(\mathbf{K} = k(\mathbf{X}, \mathbf{X})\), where \(\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_n]\)
- Predictive distribution: \(p(f(\mathbf{x}_*) | \mathbf{y}, \mathbf{X}, \mathbf{x}_*) = \mathcal{N}(\mu_*, \sigma_*^2)\)
- \(\mu_* = \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{y}\)
- \(\sigma_*^2 = k(\mathbf{x}_*, \mathbf{x}_*) - \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{k}_*\)
- \(\mathbf{k}_* = [k(\mathbf{x}_*, \mathbf{x}_1), k(\mathbf{x}_*, \mathbf{x}_2), ..., k(\mathbf{x}_*, \mathbf{x}_n)]^T\)
Classification:
Gaussian process classification models the latent function \(f(\mathbf{x})\) as a Gaussian process and defines the classification probability through this latent function. For example, in binary classification problems, the logistic function or probit function is used to transform the latent function value into a probability.
- Latent function: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\)
- Binary classification: \(p(y = 1 | f(\mathbf{x})) = \sigma(f(\mathbf{x}))\) (where \(\sigma\) is the logistic function)
In classification problems, the posterior distribution does not have a closed form, so approximate inference methods such as Laplace approximation or variational inference are used. ### 5. Gaussian Process’s Advantages and Disadvantages and Comparison with Deep Learning
Advantages:
- Quantification of Uncertainty: Provides the uncertainty of predictions in the form of predictive variance.
- Data Efficiency: Can perform well with a relatively small amount of data.
- Flexibility in Kernel Selection: Allows for the design of models tailored to the characteristics of the problem by using various kernel functions.
- Bayesian Interpretation: Naturally interpretable within the Bayesian framework.
Disadvantages:
- Computational Complexity: Has a computational complexity of \(O(n^3)\) for training data size \(n\). (Due to inverse matrix calculation)
- Model Selection: Selecting an appropriate kernel function and hyperparameters is crucial, which can be challenging.
- High-Dimensional Input: Performance may degrade in high-dimensional input spaces.
Comparison with Deep Learning:
- Data Requirements: Deep learning models generally require much more data than Gaussian processes.
- Computational Cost: Deep learning models are computationally expensive to train but relatively fast for inference. Gaussian processes are fast to train (especially with small datasets) but incur a computational cost proportional to the data size for inference.
- Uncertainty: Deep learning models typically do not provide uncertainty of predictions. (Though there are exceptions, such as Bayesian deep learning.)
- Expressiveness: Deep learning models can express very complex functions, whereas Gaussian processes have their expressiveness limited by the kernel function.
- Interpretability: Gaussian processes can explicitly state model assumptions through kernel functions and quantify the uncertainty of prediction results.
Recently, models combining deep learning and Gaussian processes (e.g., Deep Kernel Learning) are also being researched.
6.6.1 Mathematical Foundations of Uncertainty Handling
Generally, we think of a function as a single line, but the Gaussian process considers it as “a set of possible lines”. Mathematically, this is represented as:
\(f(t) \sim \mathcal{GP}(m(t), k(t,t'))\)
For example, if we consider the location of a bicycle, \(m(t)\) is the mean function that represents the prediction “it will mostly follow this path”. \(k(t,t')\) is the covariance function (or kernel) that represents “how related are the locations at different times?” There are several representative kernels. One of the most commonly used kernel functions is the RBF (Radial Basis Function).
\(k(t,t') = \sigma^2 \exp\left(-\frac{(t-t')^2}{2l^2}\right)\)
This formula is very intuitive. The closer the two time points \(t\) and \(t'\) are, the larger the value, and the farther apart they are, the smaller the value. It’s similar to “if I know the current location, I can predict the location after a while, but I don’t know the location in the distant future”.
Let’s assume the kernel (\(K\)) is RBF and look at an actual example. Suppose you have a bicycle-sharing service (or an autonomous vehicle). We want to estimate the entire moving path of the bicycle based on only a few observed GPS data points.
Basic Prediction Formula
\(f_* | X, y, X_* \sim \mathcal{N}(\mu_*, \Sigma_*)\)
This formula represents “based on the GPS records (\(X\), \(y\)) we have, the location of the bicycle at an unknown time (\(X_*\)) follows a normal distribution with mean \(\mu_*\) and uncertainty \(\Sigma_*\)”.
Location Prediction Calculation
\(\mu_* = K_*K^{-1}y\)
This formula shows how to predict the location of the bicycle. \(K_*\) represents the ‘temporal correlation’ between the predicted time point and the GPS recorded time points, \(K^{-1}\) represents the ‘weight adjustment’ considering the relationship between the GPS records, and \(y\) represents the actual GPS-recorded locations. For example, when predicting the location at 2:15 PM: 1. Refer to the GPS records (\(y\)) at 2:10 PM and 2:20 PM, 2. Consider the time difference (\(K_*\)) between each time point, 3. Reflect the temporal continuity (\(K^{-1}\)) of the GPS records.
Uncertainty Estimation
\(\Sigma_* = K_{**} - K_*K^{-1}K_*^T\)
This formula calculates the uncertainty of the location prediction. \(K_{**}\) calculates the ‘basic uncertainty’ of the predicted time point, and \(K_*K^{-1}K_*^T\) calculates the ‘decreasing uncertainty’ due to the GPS records. \(K\) is a matrix representing the relationship between existing observation data, so the value increases as the data becomes more dense. \(K_*\) represents the relationship between the new prediction point and the existing data, so it can consider more surrounding data as the data becomes more dense.
In real-world situations: 1. Initially, assume the bicycle can go anywhere (\(K_{**}\) is large) 2. As there are more GPS records (\(K_*\) increases) 3. And the records are consistent (\(K^{-1}\) becomes stable) 4. The uncertainty of the location estimation decreases.
Effect of Data on Formulas The prediction with uncertainty, depending on the amount of GPS data, appears as follows: 1. Frequent GPS recording sections: low uncertainty - \(K_*\) is large and there is a lot of data, so \(K_*K^{-1}K_*^T\) is large - Therefore, \(\Sigma_*\) is small, making the path estimation accurate 2. Infrequent GPS recording sections: high uncertainty - \(K_*\) is small and there is little data, so \(K_*K^{-1}K_*^T\) is small - Therefore, \(\Sigma_*\) is large, making the path estimation uncertain
Simply put, as the amount of dense time-interval data increases, \(K\) becomes larger, and the uncertainty decreases.
Let’s understand this using an example of predicting a bicycle path.
Code
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 시각화 스타일 설정
sns.set_style("whitegrid")
plt.rcParams['font.size'] = 10
# 데이터셋 1: 5개 관측점
time1 = np.array([0, 2, 5, 8, 10]).reshape(-1, 1)
position1 = np.array([0, 2, 3, 1, 4])
# 데이터셋 2: 8개 관측점
time2 = np.array([0, 1, 2, 4, 5, 6, 8, 10]).reshape(-1, 1)
position2 = np.array([0, 1, 2.5, 1.5, 3, 2, 1, 4]) # 더 큰 변동성 추가
# 예측할 시간점 생성: 0~10분 구간을 100개로 분할
time_pred = np.linspace(0, 10, 100).reshape(-1, 1)
# RBF 커널 함수 정의
def kernel(T1, T2, l=2.0):
sqdist = np.sum(T1**2, 1).reshape(-1, 1) + np.sum(T2**2, 1) - 2 * np.dot(T1, T2.T)
return np.exp(-0.5 * sqdist / l**2)
# 가우시안 프로세스 예측 함수
def predict_gp(time, position, time_pred):
K = kernel(time, time)
K_star = kernel(time_pred, time)
K_star_star = kernel(time_pred, time_pred)
mu_star = K_star.dot(np.linalg.inv(K)).dot(position)
sigma_star = K_star_star - K_star.dot(np.linalg.inv(K)).dot(K_star.T)
return mu_star, sigma_star
# 두 데이터셋에 대한 예측 수행
mu1, sigma1 = predict_gp(time1, position1, time_pred)
mu2, sigma2 = predict_gp(time2, position2, time_pred)
# 2개의 서브플롯 생성
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 4))
# 첫 번째 그래프 (5개 데이터)
ax1.fill_between(time_pred.flatten(),
mu1 - 2*np.sqrt(np.diag(sigma1)),
mu1 + 2*np.sqrt(np.diag(sigma1)),
color='blue', alpha=0.2, label='95% confidence interval')
ax1.plot(time_pred, mu1, 'b-', linewidth=1.5, label='Predicted path')
ax1.plot(time1, position1, 'ro', markersize=6, label='GPS records')
ax1.set_xlabel('Time (min)')
ax1.set_ylabel('Position (km)')
ax1.set_title('Route Estimation (5 GPS points)')
ax1.legend(fontsize=8)
# 두 번째 그래프 (8개 데이터)
ax2.fill_between(time_pred.flatten(),
mu2 - 2*np.sqrt(np.diag(sigma2)),
mu2 + 2*np.sqrt(np.diag(sigma2)),
color='blue', alpha=0.2, label='95% confidence interval')
ax2.plot(time_pred, mu2, 'b-', linewidth=1.5, label='Predicted path')
ax2.plot(time2, position2, 'ro', markersize=6, label='GPS records')
ax2.set_xlabel('Time (min)')
ax2.set_ylabel('Position (km)')
ax2.set_title('Route Estimation (8 GPS points)')
ax2.legend(fontsize=8)
plt.tight_layout()
plt.show()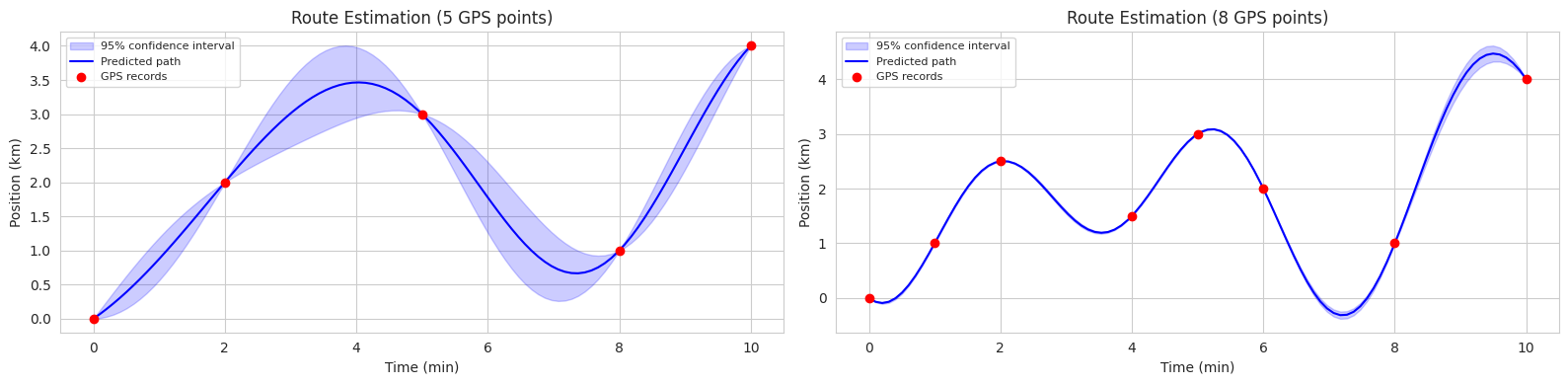
The code above is an example of using GP to estimate bicycle routes in two scenarios (5 observation points, 8 observation points). In each graph, the blue solid line represents the predicted average route, and the blue shaded area represents the 95% confidence interval.
- When there is little data (left graph): Because GPS records are sparse, the uncertainty of prediction (the width of the confidence interval) is large.
- When there is a lot of data (right graph): As GPS records become denser, the uncertainty of prediction decreases and the predicted route becomes closer to the actual route.
Thus, GP provides not only predictive results but also uncertainty, making it useful in various fields where uncertainty needs to be considered in decision-making processes (e.g., autonomous driving, robot control, medical diagnosis).
6.6.2 Modern Applications
Gaussian processes are applied in various scientific and engineering fields such as robot control, sensor network optimization, molecular structure prediction, climate modeling, and astrophysical data analysis. A representative application in machine learning is hyperparameter optimization, which we have already discussed. Another field that requires predictive uncertainty is autonomous driving. By predicting the future position of surrounding vehicles and driving more defensively in areas with high uncertainty, autonomous vehicles can improve safety. Additionally, Gaussian processes are widely used in medical fields to predict patient status changes and in asset markets to predict stock prices and manage risks based on uncertainty. Recently, GP applications have been actively researched in combination with reinforcement learning, generative models, causal inference, and meta-learning.
6.6.3 Deep Kernel Learning
The most important aspect of Gaussian processes is the kernel (covariance function). Deep learning has strengths in learning representations from data. Combining the predictive power of GP and the representation learning ability of deep learning is a natural research direction. One representative method is deep kernel learning (DKL), which uses neural networks to directly learn kernels from data instead of predefining them like RBF kernels.
The general structure of DKL is as follows:
- Feature Extraction: Input data passes through a deep neural network (usually CNN or Transformer) and is transformed into a low-dimensional feature vector.
- Kernel Computation: The extracted feature vector is used as input to calculate the kernel matrix using a Gaussian process kernel function (e.g., RBF kernel).
- Gaussian Process: The calculated kernel matrix and training data are used to learn a Gaussian process model, which performs predictions (mean and variance) on new inputs. DKL has the advantage of learning useful feature representations and data similarities simultaneously through neural networks. This enables uncertainty-aware predictions for complex data (e.g., images, graphs, text).
DKL is being applied in various fields. * Image Classification: Uses CNN to extract image features and GP to perform classification. * Graph Classification: Uses Graph Neural Network (GNN) to extract features from graph structures and GP to perform graph classification. * Molecular Property Prediction: Takes molecular graphs as input and predicts molecular properties (e.g., solubility, toxicity). * Time Series Forecasting: Uses RNN to extract features from time series data and GP to predict future values. Here, we will run a simple example of DKL and examine more detailed content and application cases in Part 2.
Deep Kernel Network
First, we define the deep kernel network. The kernel network is a neural network that learns kernel functions. This neural network takes input data and outputs feature representations. These feature representations are used to calculate the kernel matrix.
Code
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Normal
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Set seed for reproducibility
torch.manual_seed(42)
np.random.seed(42)
# Define a neural network to learn the kernel
class DeepKernel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(DeepKernel, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, hidden_dim)
self.fc3 = nn.Linear(hidden_dim, output_dim)
self.activation = nn.ReLU()
def forward(self, x):
x = self.activation(self.fc1(x))
x = self.activation(self.fc2(x))
x = self.fc3(x) # No activation on the final layer
return xThe input to a deep kernel network is typically a 2D tensor, where the first dimension is the batch size and the second dimension is the dimension of the input data. The output is a 2D tensor of shape (batch size, feature dimension).
GP Layer Definition
The GP layer takes the output of the deep kernel network and computes the kernel matrix, then calculates the predictive distribution.
Code
import torch
import torch.nn as nn
# Define the Gaussian Process layer
class GaussianProcessLayer(nn.Module):
def __init__(self, num_dim, num_data):
super(GaussianProcessLayer, self).__init__()
self.num_dim = num_dim
self.num_data = num_data
self.lengthscale = nn.Parameter(torch.ones(num_dim)) # Length-scale for each dimension
self.noise_var = nn.Parameter(torch.ones(1)) # Noise variance
self.outputscale = nn.Parameter(torch.ones(1)) # Output scale
def forward(self, x, y):
# Calculate the kernel matrix (using RBF kernel)
dist_matrix = torch.cdist(x, x) # Pairwise distances between inputs
kernel_matrix = self.outputscale * torch.exp(-0.5 * dist_matrix**2 / self.lengthscale**2)
kernel_matrix += self.noise_var * torch.eye(self.num_data)
# Calculate the predictive distribution (using Cholesky decomposition)
L = torch.linalg.cholesky(kernel_matrix)
alpha = torch.cholesky_solve(y.unsqueeze(-1), L) # Add unsqueeze for correct shape
predictive_mean = torch.matmul(kernel_matrix, alpha).squeeze(-1) # Remove extra dimension
v = torch.linalg.solve_triangular(L, kernel_matrix, upper=False)
predictive_var = kernel_matrix - torch.matmul(v.T, v)
return predictive_mean, predictive_var
return predictive_mean, predictive_varThe input to the GP layer is a 2D tensor of shape (batch size, feature dimension). The output is a tuple containing the predicted mean and variance. The RBF kernel is used for computing the kernel matrix, and Cholesky decomposition is utilized for calculating the predictive distribution to improve computational efficiency. y.unsqueeze(-1) and .squeeze(-1) are used to match the dimensions between y and the kernel matrix.
Code
# 데이터를 생성
x = np.linspace(-10, 10, 100)
y = np.sin(x) + 0.1 * np.random.randn(100)
# 데이터를 텐서로 변환
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(-1) # (100,) -> (100, 1)
y_tensor = torch.tensor(y, dtype=torch.float32) # (100,)
# 딥 커널과 GP 레이어를 초기화
deep_kernel = DeepKernel(input_dim=1, hidden_dim=50, output_dim=1) # output_dim=1로 수정
gp_layer = GaussianProcessLayer(num_dim=1, num_data=len(x))
# 손실 함수와 최적화기를 정의
loss_fn = nn.MSELoss() # Use MSE loss
optimizer = optim.Adam(list(deep_kernel.parameters()) + list(gp_layer.parameters()), lr=0.01)
num_epochs = 100
# 모델을 학습
for epoch in range(num_epochs):
optimizer.zero_grad()
kernel_output = deep_kernel(x_tensor)
predictive_mean, _ = gp_layer(kernel_output, y_tensor) # predictive_var는 사용 안함
loss = loss_fn(predictive_mean, y_tensor) # Use predictive_mean here
loss.backward()
optimizer.step()
if(epoch % 10 == 0):
print(f'Epoch {epoch+1}, Loss: {loss.item()}')
# 예측을 수행
with torch.no_grad():
kernel_output = deep_kernel(x_tensor)
predictive_mean, predictive_var = gp_layer(kernel_output, y_tensor)
# 결과를 시각화
sns.set()
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'bo', label='Training Data')
plt.plot(x, predictive_mean.numpy(), 'r-', label='Predictive Mean')
plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
alpha=0.2, label='95% CI')
plt.legend()
plt.show()Epoch 1, Loss: 4.3467857893837725e-13
Epoch 11, Loss: 3.1288711313699757e-13
Epoch 21, Loss: 3.9212150236903054e-13
Epoch 31, Loss: 4.184870765894244e-13
Epoch 41, Loss: 2.9785689973499396e-13
Epoch 51, Loss: 3.8607078688482344e-13
Epoch 61, Loss: 3.9107123572454383e-13
Epoch 71, Loss: 2.359286811054462e-13
Epoch 81, Loss: 3.4729958167147024e-13
Epoch 91, Loss: 2.7600995490886793e-13/tmp/ipykernel_1408185/2425174321.py:40: RuntimeWarning: invalid value encountered in sqrt
plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
/tmp/ipykernel_1408185/2425174321.py:41: RuntimeWarning: invalid value encountered in sqrt
predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),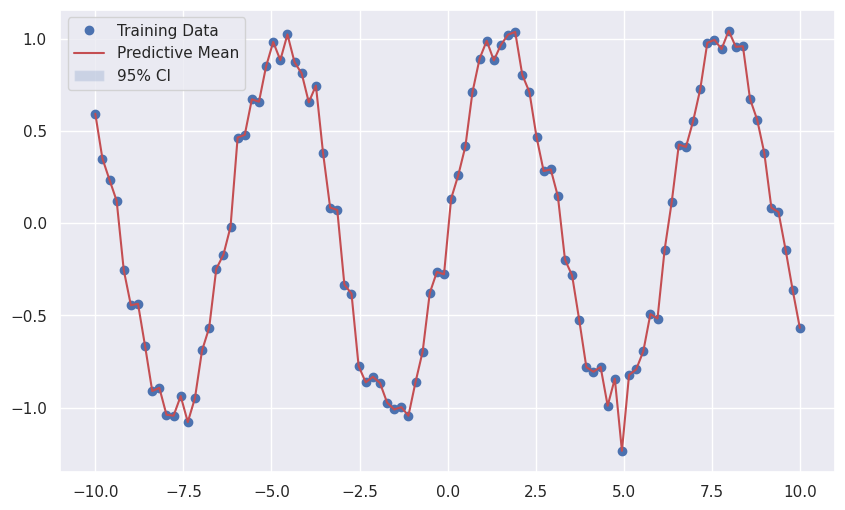
For model learning, the Mean Squared Error (MSE) loss function is used, and the Adam optimizer is used to learn the parameters of the deep kernel network and the GP layer simultaneously.
6.6.4 Possibilities and Limitations of DKL
The previous example shows the basic idea of Deep Kernel Learning (DKL). It uses a deep learning model (the DeepKernel class) to extract features from the input data and calculates the Gaussian Process (GP) kernel using these features. Then, it uses GP to calculate the mean and variance (uncertainty) of predictions. In this way, DKL combines the representation learning ability of deep learning and the uncertainty estimation ability of GP, making reliable predictions possible even for complex data.
Possibilities of DKL:
- Data Efficiency: GP tends to work well even with small amounts of data. DKL combines the powerful feature extraction capability of deep learning and the data efficiency of GP, allowing it to perform well with small amounts of data.
- Uncertainty Estimation: DKL can quantify the uncertainty of predictions. This is particularly useful in applications where safety is crucial (e.g., medical diagnosis, autonomous driving).
- Flexibility: DKL can be applied to various types of data (images, text, graphs, etc.). By freely selecting neural network architectures, it is possible to design feature extractors tailored to specific problems.
- Combination with Bayesian Optimization: DKL can be combined with Bayesian optimization to efficiently tune the hyperparameters of models.
Limitations of DKL:
- Computational Cost: GP still has a high computational cost. Especially when there is a large amount of training data, the size of the kernel matrix becomes large, making calculations difficult.
- Neural Network Design: The performance of DKL heavily depends on the design of the feature extractor (neural network). Selecting an appropriate neural network architecture remains a challenging problem.
- Lack of Theoretical Understanding: Theoretical analysis of DKL is still in its early stages. More research is needed to understand why DKL works well and under what conditions it performs well.
Conclusion
This chapter has explored various techniques for addressing the overfitting problem in deep learning models. From traditional methods such as L1/L2 regularization, dropout, and batch normalization, to advanced techniques like Bayesian optimization, Gaussian processes, and Deep Kernel Learning, deep learning research continues to evolve to improve the generalization performance of models.
Overfitting occurs when a deep learning model becomes too specialized to the training data, resulting in poor predictive performance on new data. This can happen when the model’s complexity is too high, when there is insufficient training data, or when the data contains a lot of noise. Preventing overfitting is a crucial task when applying deep learning models to real-world problems.
The various techniques introduced in this chapter approach the overfitting problem in different ways:
- Regularization: Penalizes model complexity by adding a penalty term to the loss function to prevent weights from becoming too large (L1, L2, Elastic Net).
- Dropout: Randomly removes neurons during training to prevent the model from relying too heavily on specific neurons or combinations of neurons.
- Batch Normalization: Normalizes the input to each layer, stabilizing and accelerating training.
- Hyperparameter Optimization: Uses methods like Bayesian optimization to find the optimal combination of hyperparameters that maximizes model performance.
- Gaussian Processes and Deep Kernel Learning: Explicitly models uncertainty, allowing for more reliable predictions. Properly combining these techniques and tuning them to suit the characteristics of the problem is one of the key competencies of deep learning engineers. There is no single solution that is “perfect for all cases,” and the optimal method must be found through experimentation and analysis. Deep learning research is rapidly evolving, and new techniques to address overfitting will continue to emerge.
Practice Problems
Basic Problems
- Explain the concepts of overfitting and underfitting, and describe how each phenomenon affects a model’s performance.
- Describe the differences between L1 regularization and L2 regularization, and explain how each regularization affects a model’s weights.
- Explain the working principle of dropout and describe how dropout helps prevent overfitting.
- Explain the concept of batch normalization and describe the benefits it provides to deep learning model training.
- Describe the changes in the graph when changing the lambda values in the custom_loss function.
- Define L1 and L2 norms.
- Explain how the mean and variance are calculated in the batch normalization formula, and how they are used in the normalization process.
Application Problems
- Train a polynomial regression model on a given dataset and observe the overfitting and underfitting phenomena by changing the degree of the polynomial. (Write Python code)
- Create a simple neural network model and apply L1 or L2 regularization to observe the changes in the model’s weights and compare the performance changes based on the regularization strength. (Write Python code)
- Train a neural network model with different dropout rates and compare the training/validation loss and accuracy for each rate. (Write Python code)
- Compare the learning speed and convergence stability of a neural network model by adding or removing batch normalization layers. (Write Python code)
- Use the Lagrange multiplier method to derive the optimal conditions for the L1 and L2 regularized loss function.
- Derive the backpropagation process for batch normalization and explain how it helps alleviate the vanishing gradient problem.
Advanced Problems
- Visualize the effect of L1 and L2 regularization on the loss surface and explain the geometric meaning of each regularization. (Write Python code)
- Interpret dropout from the perspective of ensemble learning and explain how dropout can be used to estimate a model’s uncertainty.
- Compare various hyperparameter optimization techniques (grid search, random search, Bayesian optimization, etc.) and explain their advantages and disadvantages.
- Implement the core idea of Bayesian optimization without using BoTorch to find the optimal value of a simple function. (Write Python code, library use allowed)
- Explain the basic principles of Gaussian processes and describe how they perform predictions with uncertainty.
- Explain the conditions that a Gaussian process kernel function must satisfy and prove that the RBF kernel satisfies these conditions.
- Explain the role of acquisition functions in Bayesian optimization and derive the Expected Improvement (EI) acquisition function formula, explaining its meaning.
Click to view contents (Exercise answers)
Exercise Answers
Basic Problems
- Overfitting/Underfitting:
- Overfitting: The phenomenon where a model is too well-fit to the training data, resulting in poor performance on new data (validation/test data). It performs well on the training data but poorly on the validation/test data.
- Underfitting: The phenomenon where a model is too simple and fails to learn the patterns in the training data. It shows low performance on both the training and validation/test data.
- L1/L2 Regularization:
- L1 Regularization (Lasso): Adds the absolute value sum of weights to the loss function. \(\lambda \sum_{i} |w_i|\) Makes some weights exactly 0, resulting in feature selection.
- L2 Regularization (Ridge): Adds the square sum of weights to the loss function. \(\lambda \sum_{i} (w_i)^2\) Makes weights close to 0 but not exactly 0.
- Dropout:
- Mechanism: Randomly deactivates some neurons during training by setting their output to 0.
- Preventing Overfitting: Trains with different neuron combinations each time, preventing dependence on specific neurons and achieving ensemble learning effects.
- Batch Normalization:
- Concept: Normalizes the input of each layer to have a mean of 0 and a variance of 1.
- Benefits: Improves training speed, alleviates vanishing/exploding gradient problems, allows for higher learning rates, and has some regularization effect.
custom_lossLambda Change:- Increasing
lambda: Increases the influence of the regularization term. Weights become smaller, and the model becomes simpler, increasing the risk of underfitting. - Decreasing
lambda: Decreases the influence of the regularization term. Weights become larger, and the model becomes more complex, increasing the risk of overfitting.
- Increasing
- L1/L2 Norm:
- L1 Norm: The sum of the absolute values of vector elements. \(\| \mathbf{x} \|_1 = |x_1| + |x_2| + \dots + |x_n|\)
- L2 Norm: The square root of the sum of the squares of vector elements (Euclidean distance). \(\| \mathbf{x} \|_2 = \sqrt{|x_1|^2 + |x_2|^2 + \dots + |x_n|^2}\)
- Batch Normalization Formula:
- Mean (μ): The mean of samples in a mini-batch. \(\mu = \frac{1}{m} \sum_{i=1}^{m} x_i\)
- Variance (σ²): The variance of samples in a mini-batch. \(\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu)^2\)
- Normalization: \(x_{i\_\text{norm}} = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\) (ε is a small constant to prevent division by zero)
Applied Problems
Polynomial Regression: (Code omitted) If the degree is too high, it overfits; if it’s too low, it underfits.
L1/L2 Regularization: (Code omitted) The stronger the regularization strength (
lambda), the smaller the weights become, and performance changes are observed.Dropout Ratio: (Code omitted) An appropriate dropout ratio can prevent overfitting and improve performance. Too high a ratio can cause underfitting.
Batch Normalization: (Code omitted) Adding batch normalization tends to speed up learning and stabilize convergence.
Lagrange Multiplier Method:
- L2 Regularization: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_2^2 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + 2\lambda\mathbf{w} = 0\)
- L1 Regularization: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_1 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + \lambda \cdot \text{sign}(\mathbf{w}) = 0\) (sign(w) is the sign of w)
Batch Normalization Backpropagation: (derivation omitted) Batch normalization normalizes the input to each layer, mitigating the vanishing/exploding gradient problem and stabilizing learning.
Advanced Problems
Loss Plane Visualization: (code omitted) L1 regularization creates a diamond-shaped constraint, while L2 regularization creates a circular constraint, resulting in different optimal solutions.
Dropout Ensemble: Dropout has the effect of training a different network structure each time, similar to ensemble learning. During prediction, all neurons are used (without dropout) to perform an average prediction. Monte Carlo dropout can be used to estimate the uncertainty of predictions.
Hyperparameter Optimization Techniques:
- Grid Search: Try all combinations. Computational cost is very high.
- Random Search: Try random combinations. Can be more efficient than grid search.
- Bayesian Optimization: Use a probabilistic model based on previous search results to determine the next search point. Efficient.
Bayesian Optimization Implementation: (code omitted) Use a surrogate model (e.g., Gaussian process) and an acquisition function (e.g., Expected Improvement) to implement.
Gaussian Process: A probability distribution over functions. Define the covariance between function values using a kernel function. Calculate the posterior distribution based on given data to provide the mean and variance (uncertainty) of predictions.
Kernel Function Conditions: Must satisfy positive semi-definiteness. The kernel matrix (Gram matrix) generated for arbitrary input points must be a positive semi-definite matrix. The RBF kernel satisfies this condition. (proof omitted)
Acquisition Function: Used to determine the next search point in Bayesian optimization. Expected Improvement (EI) considers the possibility of obtaining better results than the current optimal value and the degree of improvement, selecting the next search point accordingly. (equation derivation omitted)
- Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): The original paper explaining the concept and effect of dropout. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf)
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): The original paper explaining the concept and effect of batch normalization. (https://arxiv.org/abs/1502.03167)
- Deep Learning (Goodfellow et al., 2016): A deep learning textbook that discusses overfitting and regularization techniques in detail in Chapter 7 “Regularization for Deep Learning”. (http://www.deeplearningbook.org/)
- Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Explains the difficulties in training early deep learning models and the importance of weight initialization methods. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
- Regularization techniques for deep learning: A survey (Kukacka et al., 2017): A paper that comprehensively compares and analyzes various regularization techniques.
- A Tutorial on Bayesian Optimization (Frazier, 2018): A tutorial explaining the basic concepts and applications of Bayesian optimization. (https://arxiv.org/abs/1807.02811)
- Bayesian Optimization (Garnett, 2023): A comprehensive textbook on Bayesian optimization (https://www.bayesoptbook.com/)
- Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): A textbook that covers the basic principles of Gaussian processes and their applications in machine learning. (http://www.gaussianprocess.org/gpml/)
- Deep Kernel Learning (Wilson et al., 2016): A paper explaining the concept and method of deep kernel learning. (https://arxiv.org/abs/1511.02222)
- Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): A hands-on machine learning and deep learning textbook that explains overfitting and regularization techniques with actual code examples.
- Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): A paper on the Adam optimizer
- Decoupled Weight Decay Regularization (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): A paper on AdamW
- Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): This original paper explains the concept and effect of dropout. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf)
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): This original paper explains the concept and effect of batch normalization. (https://arxiv.org/abs/1502.03167)
- Deep Learning (Goodfellow et al., 2016): A deep learning textbook that covers overfitting and regularization techniques in detail in Chapter 7 “Regularization for Deep Learning”. (http://www.deeplearningbook.org/)
- Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Explains the difficulty of learning early deep learning models and the importance of weight initialization methods. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
- Regularization techniques for deep learning: A survey (Kukacka et al., 2017): A paper that compares and analyzes various regularization techniques.
- A Tutorial on Bayesian Optimization (Frazier, 2018): A tutorial that explains the basic concepts and applications of Bayesian optimization. (https://arxiv.org/abs/1807.02811)
- Bayesian Optimization (Garnett, 2023): A comprehensive textbook on Bayesian optimization. (https://www.bayesoptbook.com/)
- Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): A textbook that covers the basic principles of Gaussian processes and their applications in machine learning. (http://www.gaussianprocess.org/gpml/)
- Deep Kernel Learning (Wilson et al., 2016): A paper that explains the concept and method of deep kernel learning. (https://arxiv.org/abs/1511.02222)
- Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): A hands-on machine learning and deep learning textbook that explains overfitting and regularization techniques with actual code examples.
- Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): A paper on the Adam optimizer. Decoupled Weight Decay Regularization (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): A paper on AdamW
There is no original text to translate.